Archive
What is the Physical Meaning of the Levi-Civita Connection?
A Riemannian manifold is a differentiable manifold endowed with a Riemannian metric. Given a Riemannian metric, the lengths of curves can be defined via integration, and the angle of intersection of two curves is also well defined. However, there is a priori no direct way of aligning neighbouring tangent planes, hence no direct way of measuring acceleration, for example.
A connection defines the rate-of-change of a vector field. There are many possible connections, hence it is natural to ask what connection to use, and whether on a Riemannian metric there is a canonical choice of a connection. The answer to the first question is, of course, that it depends on what you are wanting to do. (On a Lie group there are several interesting connections, for example.) This short note focuses on the second question.
The canonical choice of a connection on a Riemannian manifold is the Levi-Civita connection. Why is it a natural choice though, and what is its physical meaning?
The short answer is that it corresponds to the parallel transport which would naturally occur if we were living on this manifold. For example, if we are told to walk in a straight line with zero acceleration, we could do this on our planet without defining a connection. How? We simply place one foot in front of the other to take our first step, then repeat, each time doing our best to walk in a straight line. What actually happens is gravity pulls our foot back to Earth and hence we end up walking in a great circle.
Similarly, if we walk while holding a lance, and are told not to move the lance as we walk, we are actually defining a rule for parallel transport.
Put simply, the Levi-Civita connection corresponds to the rule for parallel transport that results by walking along the curve without moving the vector/lance. Gravity will cause additional movement to ensure we stay on the surface of the planet and this is what is captured by the Levi-Civita connection.
Technically, it is not gravity but merely projection back onto the surface of the manifold. Specifically, by the Nash embedding theorem, any Riemannian manifold can be isometrically embedded into Euclidean space. Then walking “in a straight line” on the manifold is achieved by taking a step in Euclidean space then projecting back down to the manifold (just as gravity would pull your foot back to the ground). Then take the limit as the step size goes to zero.
For additional details, see my response here: https://mathoverflow.net/questions/376486/what-is-the-levi-civita-connection-trying-to-describe/376593#376593
The Twin Capacitor Paradox
With COVID-19 causing a transition to online teaching, I am now in the habit of making short videos…
Consider two isolated capacitors, one with a charge on it, one without. Then suddenly bring them together. The charge will distribute equally on the two capacitors. But energy will have been lost! Where did it go?
A Note on Duality in Convex Optimisation
This note elaborates on the “perturbation interpretation” of duality in convex optimisation. Caveat lector: regularity conditions are ignored.
Recall that in convex analysis, a convex set is fully determined by its supporting hyperplanes. Therefore, any result about convex sets should be re-writable in terms of supporting hyperplanes. This is the basis of duality. A simple yet striking example is Fenchel duality which is nicely illustrated in the Wikipedia. Although it relies on the Legendre transform, which I have written about here, the current note is self-contained: it explains the Legendre transform from first principles.
Let’s start with a classic example of duality. In its usual presentation, it is not at all clear that it relates to the aforementioned duality between convex sets and their hyperplanes. Nevertheless, before presenting a general method for taking the dual of a problem, it is useful to have a concrete example at hand.
Consider minimising subject to
where
are convex functions and
is a vector in
. The dual of this problem is
. A number of remarks are made below.
Remark 1.1: One way to “understand” this duality is by understanding when it is permissible to replace by
. Such results go by the name of minimax theorems. Intuitively, if
has a single critical point that is a saddle point (with the correct orientation) then
can be replaced by
. (And it is always true that
.) If we assume
equals
then it becomes straightforward to verify the dual gives the correct answer. Indeed,
equals
if
and equals
if
. Therefore,
equals
if
and equals
otherwise. Therefore, the unconstrained minimisation of
is equivalent to the constrained minimisation of
subject to
. However, this is by no means the end of the story. It is not even the beginning!
Remark 1.2: The dual appears to relate to the method of Lagrange multipliers. (See here for the physical significance of the Lagrange multiplier.) This makes sense because there are only two cases. Either the global minimum of occurs at a point
which satisfies the constraint, in which case the problem reduces to an unconstrained optimisation problem, or the optimum feasible solution
satisfies the equality constraint
, thereby suggesting a Lagrange multiplier approach. Again though, this is not the start of the story, although the following remarks do elaborate in this direction.
Remark 1.3: If the global minimum of occurs at a point
which satisfies the constraint
then we can check what the solution to the dual
looks like, as follows. Let
. If
then
. If
then
because
implies
. Therefore, the largest value of
occurs when
, showing that the dual
reduces to the correct solution
in this case.
Remark 1.4: If the global minimum of is infeasible (it does not satisfy the constraint
), we can reason as follows. The function
is convex. Provided
are sufficiently nice (e.g., strictly convex and differentiable), and
is bounded from below, the minimum of
occurs when
. We recognise this as the same condition occurring in the method of Lagrange multipliers for solving the constrained problem of minimising
subject to
. This Lagrange multiplier interpretation means that, for a given
, solving
gives an
which is the minimum of
subject to
for some
and not necessarily for
. Specifically, if
satisfies
then
minimises
subject to
. For reference, denote by
the optimal solution, that is,
and
. Treating
as a function of
, consider the values of
compared with
. We want to show
so that the dual problem finds the correct solution. Now,
, as required.
Remark 1.5: A benefit of the dual problem is that it has replaced the “complicated” constraint by the “simple” constraint
.
While we have linked the dual problem with Lagrange multipliers to explain what was going on, it is somewhat messy and requires additional assumptions such as differentiability. Furthermore, the dual problem was written down, rather than derived. The remainder of this note attempts to rectify these issues.
The Legendre Transform and Duality
Let be a convex function; in all that follows, the domain can be
(or some other vector space) but we study the
case for simplicity, and because no intuition is lost. Shading in the graph of
produces its epigraph —
— which is convex. The supporting hyperplanes of the epigraph of
therefore determine the epigraph of
and therefore
itself is determined by these supporting hyperplanes.
We will be lazy and write “supporting hyperplane of ” to mean a supporting hyperplane of the epigraph of
.
A hyperplane is of the form for constants
. (In higher dimensions, we would write
.) Since for any given “orientation”
there is at most one supporting hyperplane, we can define a function
by the condition that, for any given orientation
, the plane
, when shifted down by
to become
, is a supporting hyperplane of (the epigraph of)
. (If there is no such hyperplane then we will see presently it is natural to define
to be infinity.)
It is straightforward to derive a formula for . Imagine superimposing the line
onto the graph of
. If the line intersects the interior of the epigraph of
then it must be shifted down until it just touches the graph of
without entering the interior of the epigraph. If the line does not touch the graph at all, it must be shifted up until it just touches. The amount of shift can be determined by examining, for each
, the distance between the line and the graph. This distance is
, and the following calculation shows we want to maximise this quantity.
For to be a supporting hyperplane of
, it must satisfy two requirements. First, we must have that
for all
. This means
must satisfy
for all
, or in other words,
. The second requirement is that the line should intersect the graph, or in other words,
should be the smallest possible constant for which the first requirement holds. That is,
is such that
is a supporting hyperplane of
, and indeed, it is the unique supporting hyperplane with orientation
.
We therefore define . It is called the Legendre transform of
.
The original claim is that can be recovered from its supporting hyperplanes. That is, given
, we should be able to determine
. We can do this point by point. Given an
, we know that
must lie above all the supporting hyperplanes
. That is, we have
. Additionally, we know
should touch at least one supporting hyperplane, therefore,
.
It is striking that this formula has exactly the same form as the Legendre transform! Indeed, the Legendre transform is self-dual: the above can be rewritten as .
At this juncture, it is easy to state the algebra behind taking the dual of an optimisation problem. In my opinion though, there is more to be understood than just the following algebra. The remainder of this note therefore elaborates on the following.
Given a convex function that we wish to minimise, we can write down a dual optimisation problem in the following way. First, we embed
into a family of convex cost functions
meaning we choose a function
that is convex and for which
. Different embeddings can lead to different duals!
For reasons that will be explained later, the “trick” is to define and then write down an expression for
. Since the Legendre transform is self-dual,
gives the answer to the original optimisation problem.
By definition, . Also by definition,
. We therefore arrive at the following.
Duality: .
While the above algebra is straightforward, a number of questions remain.
- What is going on geometrically?
- Why should the left-hand side be easier to evaluate than the right-hand side?
- How should the family
be chosen?
It is remarked that if we are allowed to interchange and
then the left-hand side becomes
and
equals infinity unless
, so that
.
A Geometrical Explanation
The aim is to understand geometrically what the left-hand side of the equation labelled Duality is computing. Start with the term . From our discussion about the Legendre transform, we recognise this term as being the amount by which to shift the plane
to make it a supporting hyperplane for the graph
. (I like to imagine
as the quadratic function
and I think of holding a sheet of paper to the surface of
, thereby forming a tangent plane which is the same thing as a supporting hyperplane in this case.) Indeed,
where
is the Legendre transform of
.
For a given , the supporting hyperplane
touches (and, if
is smooth, is “tangent” to)
at points
that achieve the supremum in the definition of the Legendre transform, that is, at points
satisfying
. Equivalently, these are the points
achieving the infimum in
.
The first key observation is that because the hyperplane does not vary in
, if it touches the graph of
at
then
must minimise
. Intuitively, this is because the derivative of the hyperplane in the
direction being zero implies the derivative of
in the
direction (if it exists) must also be zero at the point of contact between the hyperplane and the graph. More formally, it is a straightforward generalisation of the property of the Legendre transform that
. Visually,
states that the minimum of
can be found by starting with a horizontal line and raising or lowering it until it becomes tangent to
. Algebraically, it follows immediately from the definition of the Legendre transform:
.
To prove the assertion that minimises
, fix an orientation
and assume
satisfies
. Define
. Then
. Now,
, showing that
, implying
. The previous paragraph tells us that
, hence
, as claimed.
We are halfway there. Given an orientation , we can implicitly find a point
by solving the optimisation problem
. We know for any such point
,
minimises
. Therefore, if we can find a
such that
then we are done.
To help focus on the implicit function , rewrite
as
. By defining
, we get
. We want to find
such that the point
achieving the supremum in
satisfies
. That is, we want to find
such that
. Rewriting in terms of
gives the condition
. We can solve this either geometrically or algebraically.
Geometrically, recall that is the location on the vertical axis where the hyperplane with orientation
intersects the vertical axis. Visually consider a tangent line of the convex function
. As we vary the tangent point, we observe where the tangent line intersects the
-axis. It is visually clear that the maximum intersection point occurs when
. We therefore expect that the solution to
is the value of
that maximises
.
Algebraically, start by recalling from earlier that we have shown a property of the Legendre transform is that . What we want is the “dual” of this property, obtained via the substitution
, namely
. Since the Legendre transform is self-dual,
, and in particular, we have deduced that
, agreeing with our geometric intuition in the previous paragraph.
What we have shown is that if maximises
then the infimum in
is achieved at a point
with
. Indeed, assume
maximises
. Retracing ours steps shows that
and since
and
we have that
. If
minimises
, so that
, then
showing
achieves the infimum.
Summary: To find , we first find the intercept point
of a hyperplane with orientation
. We then vary
until the intercept point is as large as possible:
. We know from earlier that the corresponding hyperplane will tangentially intersect the graph of
at a point
where
(because
has been maximised) and where
minimises
(because the hyperplane does not vary in
). Since the infimum is achieved at
, the value of
is readily determined by substituting in
. Specifically,
. This concludes our geometric interpretation of the Duality equation.
Remark: While introducing points at which the infimum is achieved in the Duality equation is essential for giving geometrical intuition, it is a hindrance when it comes to algebraic derivations. Indeed, the infimum need not be achieved at any point, or it may be achieved at multiple points. This is the natural tension in mathematics between intuitive explanations and rigorous (but not necessarily intuitive) algebra.
An Example of When the Dual Problem is Simpler
The Duality equation is only useful if solving for various
were easier than solving
. Naively, one might assume this is never the case! Indeed,
appears to contain the original optimisation problem! But this reasoning is flawed: the optimisation problem could be written equally well as
, and an example is now given of where
is easier to evaluate than
.
Consider the constrained optimisation problem introduced near the start of this note: minimise subject to
. The “discontinuity” at the boundary
causes difficulties: unconstrained optimisation (of continuous convex functions!) is generally easier than constrained optimisation. For reasons that will be discussed in the next section, we introduce a family of optimisation problems, indexed by
, where the objective function
stays the same but the constraints vary with
, namely,
. (The choice of negative sign is for later convenience.)
In convex optimisation, a constrained optimisation problem can be written as an unconstrained (but discontinuous and therefore still “difficult”) optimisation problem simply by defining the value of the function to be infinity at points violating the constraint. One way to write this is as because the supremum will equal zero if
, and will equal
otherwise. We therefore define our embedding to be
, so that
is the minimum of
subject to
.
Consider evaluating . The infimum over all
is equal to the minimum of the infimum over
and the infimum over
. If
then
and
. If
then
and
. Therefore,
. The last infimum equals
if
and equals
otherwise. Both
and
are easier to evaluate than the original
.
Finally, it is mentioned that for this example, the left-hand side of the Duality equation becomes . This is precisely the dual problem introduced at the start of this note.
How to Choose an Embedding?
First, a remark. One might ask, why not look for a function such that
? In principle, it seems necessary to know
before such an extension could be made, thereby rendering the extension unhelpful for computing
. The benefit of the Duality equation is that
just needs to be convex.
Since choosing an extension so that
is easier to evaluate than
comes down to experience, what we do here is analyse in greater detail the choice in the previous section.
To aid visualisation, assume we wish to minimise subject to
. Therefore,
equals
for
and equals
for
.
Simply replicating for other values of
, meaning choosing
, does not simplify the optimisation problem. Since the main difficulty is that
contains jumps to infinity, the first thing we might aim for, is ensuring
for all
.
We cannot arbitrarily choose values for because
must be convex: we must extend
while maintaining convexity and so
must depend on
.
Taking for
ensures
for all
, but
will not be convex because, for a fixed
,
would equal
for
but equal
for
. At least on one side, say,
, we must have
if
.
With these thoughts in mind, we are led to consider choosing to be
for
and
for
. This gives us a convex function satisfying
for all
. Up to a change of sign, it corresponds with the choice in the previous section.
The reader is encouraged to visualise the graph of . Note that the graph of
is obtained simply by rotating the graph of
about the
-axis, alternatively described as “tilting”
forwards or backwards. Therefore,
is the global minimum of
, while
is the global minimum of a tilted version of
.
There is an interesting interpretation of duality in this particular case. Consider . When
this corresponds to finding the unconstrained minimum of
. If
is now slowly decreased, so that
tilts forwards,
is now solving the constrained problem of minimising
subject to a constraint
where
is smaller than the location of the global minimum of
. (As
decreases, so does
.) In this way, by continuously varying
, we can increase the severity of the constraint and thereby track down the constrained minimum that we seek.
Simple Explanation for Interpretation of Lagrange Multiplier as Shadow Cost
Minimising subject to
can be solved using Lagrange multipliers, where
is referred to as the Lagrangian. The optimal value
satisfies both
and
. Although
was added to the problem, it turns out that
has physical significance: it is the rate of change of the optimal value
to perturbations
around zero in the constraint
. A simple explanation (rather than an algebraic proof) is given below.
First the reader is reminded why the condition is introduced. Let
denote the constraint set. Then
restricted to
has a local minimum at a point
if small perturbations that remain on
do not decrease
. In other words, the directional derivative of
should be zero in directions tangent to
at
. Since
is normal to the surface
at
, the directions
tangent to
at
are those satisfying
. The directional derivative at
in the direction
is
. The condition is thus that
for all
satisfying
. This condition is equivalent to requiring that
is a scalar multiple of
, that is,
for some scalar
.
To understand the physical significance of , it helps to think in terms of contour lines (or level sets) for both
and
. For concreteness, visualise the constraint set
as a circle. Let
denote the minimum achievable value of
subject to
. Then the level sets
may be visualised as ellipses whose sizes increase with
. Furthermore, if
then the level set is tangent to the constraint set (the circle), while if
then the level set
does not intersect the constraint set (the circle).
The key point is to consider what happens if we change the constraint set (the circle) from to
for some
close to zero. Changing
will perturb the circle. If the circle gets slightly bigger then we can find a new
, close to the old one, lying on the perturbed circle for which
is smaller than before. Since the gradient represents the direction of greatest increase, it seems sensible to assume the new minimum is at
for some
. We must choose
so
satisfies the new constraint:
. To first order,
. That is,
is given by solving
.
The new value of the objective function, to first order, is given by . Since
, we get that the improvement in
is
. The rate-of-change of the improvement in
with respect to a change
in the constraint is precisely
, as we set out to show.
Note that the above is not a proof but rather a rule of thumb that aids in our intuition. An actual proof is straightforward but not so intuitive.
Tennis: Attacking versus Defending
What is an attacking shot? Must an attacking shot be hit hard? What about a defensive shot? This essay will consider both the theory and the practice of attacking and defensive shots. And it will show that if you often lose 6-2 to an opponent then only a small amount of improvement might be enough to tip the scales the other way.
Tennis is a Game of Probabilities
Humans are not perfect. Anyone who has tried aiming for a small target by hitting balls fed from a ball machine will know that hitting identical balls will produce different outcomes. What is often not appreciated though is how sensitive the outcome of a tennis match is to small improvements.
Imagine a match played between two robots, where on average, out of every 20 points played, one robot wins just a single more point than the other robot. This is a very small difference in abilities. Mathematically, this translates to the superior robot having a probability of 55% of winning a point against the inferior robot. (I have used robots as a way of ignoring psychological factors. While the effects of psychological factors are relatively small, at a professional level where differences in abilities are so small to begin with, psychological factors can be crucial to determining the outcome of a match.)
Using the “Probability Calculator” found near the bottom of this page, we find that such a subtle difference in abilities translates into the superior robot winning a 5-set match 95.35% of the time. (The probability of winning a 3-set match is 91%.)
The graphs found on this page show that the set score is “most likely” to be 6-2 or 6-3 to the superior robot, so the next time you lose a match 6-2 or 6-3, believe that with only a small improvement you might be able to tip the scales the other way!
The In-Rally Effect of a Shot
While hitting a winner is a good (and satisfying) thing, no professional tries to hit a winner off every ball. Tennis is a game of probabilities, where subtle differences pay large dividends.
The aim of every ball is to increase the probability of eventually winning the point.
So if your opponent has hit a very good ball and you feel you are in trouble, you might think to yourself that you are down 30-70, giving yourself only 30% chance of winning the rally. Your aim with your return shot is to increase your odds. Even if you cannot immediately go back to 50-50, getting to 40-60 will then put 50-50 within reach on the subsequent shot.
So why not go for winners off every ball? If you can maintain a 55-45 advantage off each ball you hit, you will have a 62.31% chance of winning the game, an 81.5% chance of winning the set, and a 91% chance of winning a 3-set match. On the other hand, against a decent player, hitting a winner off a deep ball is difficult and carries with it a significant chance of failure, i.e., hitting the ball out. Studies have shown that even the very best players cannot control whether a ball narrowly falls in or narrowly falls out, meaning that winners hit very close to the line are rarely intentional but rather come from a shot aimed safely within the court that has drifted closer to the line than intended.
Attacking Options
If by an attacking ball we mean playing a shot that gives us the upper hand in the rally, then our shot needs to make it difficult for our opponent to hit a challenging ball for us. How can this be done?
First, our ability to hit an accurate ball relates to how well we are balanced, how much time we have to react, how fast the incoming ball is, the spin on the ball and the height of the ball at contact. So we can make it difficult for opponents in many different ways. The opponent’s balance can be upset by
- wrong-footing her;
- making her cover a relatively long distance in a short amount of time to reach the ball;
- jamming her by hitting straight at her;
- forcing her to move backwards (so she cannot transfer her weight forwards into the ball).
The opponent’s neurones can be given a harder task by
- giving her less time to calculate how to swing the racquet;
- varying the incoming ball on each shot (different spins, heights, depths, speeds);
- making it harder for her to predict what we will do;
- getting her thinking about other things (such as the score).
Due to our physical structure, making contact with the ball outside of our comfort zone (roughly, between knee to shoulder height) decreases the margin for error because it is harder to “flatten out” the trajectory of the racquet about the contact point.
These observations lead to a variety of strategies for gaining the upper hand, including the following basic ones.
- Take the ball early, on the rise, to take time away from the opponent.
- Hit sharp angles, going near the lines.
- Hit with heavy top-spin to get the ball to bounce above the opponent’s shoulder.
- Hit hard and flat.
- Hit very deep balls close to the baseline.
Each of these strategies carries a risk of hitting out, therefore, it is generally advised not to combine strategies: if you take the ball on the rise, do not also aim close to the lines or hit excessively hard, for example.
If you find yourself losing to someone but not knowing why, it is because subtle differences in the balls you are made to hit can increase the chances of making a mistake, and only very small changes in probability (such as dropping from winning 11 balls out of 20 to only 10 balls out of 20) can hugely affect the outcome of the match (such as dropping from a 91% chance of winning the 3-set match to only a 50% chance of winning). To emphasise, if your opponent takes the ball earlier than normal, you are unlikely to notice the subtle time difference, but over the course of the match, you will feel you are playing worse than normal.
If you are hitting hard but all your balls are coming back, remember that it is relatively easy to return a hard flat ball: the opponent can shorten her backswing yet still hit hard by using your pace, making a safe yet effective return. Hit hard and flat to the open court off a high short ball, but otherwise, try hitting with more top-spin.
Defensive Options
Just as an attacking ball need not be a fast ball, a defensive ball need not be a slow ball. Rather, a defensive ball is one where our aim is to return to an approximately 50-50 chance of winning the point. If we are off balance, or are facing a challenging ball, we cannot go for too much or we risk hitting out and immediately losing the point.
Reducing the risk of hitting out can be achieved in various ways.
- Do not swing as fast or with excessive spin.
- Take the ball later after the bounce, giving it more time to slow down.
- Block the ball back (perhaps taking it on the rise) to a safe region well away from the lines.
- Focus on being balanced, even if it means hitting with less power.
Importantly, everyone is different, and you should learn what your preferred defensive shots are. For example, while flat balls inherently have a lower margin for error, nonetheless some people may find they are more accurate hitting flat than hitting with top-spin simply due to their biomechanical structure and past practice.
Placement of a defensive shot is crucial. Because speed, spin and/or time have been sacrificed for greater safety, it is quite likely that if the opponent has time to get into a comfortable position they can punish your ball. This is yet another example of where small differences can have large consequences: if the opponent can step into the ball you might be in trouble, yet hitting just a metre deeper, or a metre further to the side, might prevent this. Moreover, never forget that placement is relative to where the opponent currently is: hitting deep to the backhand is normally a good shot unless the opponent is already there!
Changes in depth can be very effective but they must be relative to where the opponent is. If an opponent is attacking, she might have moved to being on the baseline, looking to take the next ball early. Hitting a deep top-spin shot, not necessarily very hard, is very effective in this scenario because the opponent is forced to move backwards and thus cannot generate as much power. (A skilled opponent can still hit hard, but even a 10 km/h reduction in ball speed makes a large difference.)
Technical Considerations
Watching the slow-motion clips on YouTube of professional players hitting groundstrokes shows that the same player has many different ways of hitting her forehand and backhand. At the point of contact, you can look to see where her feet are, which way her hips are pointing, which way her shoulders are pointing, the angle of her wrist, and the contact point of the ball relative to the body. And as she hits, you can look to see which parts of the body are moving and which have momentarily become static.
While an upcoming article may consider such technical aspects in greater detail, here it is simply noted that while you should be able to hit every kind of shot from any reasonable contact point, each has advantages and disadvantages. And since tennis is a game of probabilities, it comes as no surprise that the top players instinctively know not just what type of shot to hit but also how technically to hit it in the best possible way for them at that particular moment: if they have time, and want to hit a heavy top-spin, they will probably choose a contact point further away from their body and step into the ball, while if they must return a very fast ball, they may instead use a more open stance and hit the ball more in line with their eyes, well out in front.
Next time you are on the court, experiment with how changing the contact point (even over a relatively small range of 10–20 cm) can change how hard you can hit the ball, how accurately you can hit the ball, and how much top-spin you can generate. And do not forget, this may change depending on the type of incoming ball. For example, generating pace off a slow ball is better done using a different technique than returning a fast incoming ball. Failing to recognise this may mean you “feel” you are not hitting the ball well when in fact you are just not using the best technique for the particular type of shot you want to hit.
The other side of the coin is recognising that sometimes it is necessary to play a ball using a non-optimal technique due to a funny bounce, or lack of time (or inherent laziness). In this situation, it is important to adjust the type of shot you hit. If you are forced to return a hard-hit ball at full stretch, you will lose accuracy, so do not go anywhere near the lines. If you are jammed, you are not going to be able to hit as heavy a ball as you may wish, so you may change to hit flatter, opting to take time away from the opponent. Of course, changing from heavy to flat generally means changing where you want your shot to land: a shorter top-spin that bounces above shoulder height is generally good whereas a shorter flat shot is generally bad, for example.
Does the Voltage Across an Inductor Immediately Reverse if the Inductor is Suddenly Disconnected?
Consider current flowing from a battery through an inductor then a resistor before returning to the battery again. What happens if the battery is suddenly removed from the circuit? Online browsing suggests that the voltage across the inductor reverses “to maintain current flow” but the explanations for this are either by incomplete analogy or by emphatic assertion. Moreover, one could argue for the opposite conclusion: if an inductor maintains current flow, then since the direction of current determines the direction of the voltage drop, the direction of the voltage drop should remain the same, not change!
To understand precisely what happens, it is important to think in terms of actual electrons. When the battery is connected, there is a stream of electrons being pushed out of the negative terminal of the battery, being pushed through the resistor, being pushed through the inductor then being pulled back into the battery through its positive terminal. The question is what happens if the inductor is ripped from the circuit, thereby disconnecting its ends from the circuit. (The explanation of what happens does not change in any substantial way whether it is the battery or the inductor that is removed.)
The analogy of an inductor is a heavy water wheel. The inductor stores energy in a magnetic field while a water wheel stores energy as rotational kinetic energy. But if we switch off the water supply to a water wheel, and the water wheel keeps turning, what happens? Nothing much! And if we disconnect an inductor, so there is no “circuit” for current to flow in, what can happen?
One trick is to think not of a water wheel but of a (heavy) fan inside a section of pipe. Ripping the inductor out of the circuit corresponds to cutting the piping on either side of the fan and immediately capping the ends of the pipes. This capping mimics the fact that electrons cannot flow past the ends of wires; not taking sparks into consideration. Crucially then, when we disconnect the fan, there is still piping on either side of the fan, and still water left in these pipes.
Consider the water pressure in the capped pipe segments on both sides of the fan. Assume prior to cutting out the fan, water had been flowing from right to left through the fan. (Indeed, when the pump is first switched on, it will cause a pressure difference to build up across the fan. This pressure difference is what causes the fan to start to spin. As the fan spins faster, this pressure difference gets less and (ideally) goes to zero in the limit.) Initially then, there is a higher pressure on the right side of the fan. The fan keeps turning, powered partly by the pressure difference but mainly by its stored rotational kinetic energy. (Think of its blades as being very heavy, therefore not wanting to slow down.) So water gets sucked from the pipe on the right and pushed into the pipe on the left. These pipes are capped, therefore, the pressure on the right decreases while the pressure on the left increases. “Voltage drop” is a difference in pressure, therefore, the “voltage drop” across the “inductor” is changing.
There is no discontinuous change in pressure! The claim that the voltage across an inductor will immediately reverse direction is false!
That said, the pressure difference is changing, and there will come a time when the left pipe will have a higher pressure than the right pipe. Now there are two competing forces: the stored kinetic energy in the fan wants to keep pumping water from right to left, while the larger pressure on the left wants to force water from left to right. The fan will start to slow down and eventually stop, albeit instantaneously. At the very moment the fan stops spinning, there is a much larger pressure on the left than on the right. Therefore, this pressure difference will force the fan to start spinning in the opposite direction!
Under ideal conditions then, the voltage across the inductor will oscillate!
Why should we believe this analogy though? Returning to the electrons, the story goes as follows. Assume an inductor, in a circuit, has a current flowing through it, from left to right. Therefore, electrons are flowing through the inductor from right to left (because Benjamin Franklin had 50% chance of getting the convention of current flow correct). If the inductor is ripped out of the circuit, the magnetic field that had been built up will still “push” electrons through the inductor in an attempt to maintain the same current flow. The density of electrons on the right side of the inductor will therefore decrease, while the density on the left side will therefore increase. Electrons repel each other, so it becomes harder and harder for the inductor to keep pushing electrons from right to left because every electron wants its own space and it is getting more and more crowded on the left side of the inductor. Eventually, the magnetic field has used up all its energy trying to cram as many electrons as possible into the left side of the inductor. The electrons on the left are wanting to get away from each other and are therefore pushing each other over to the right side of the inductor. This “force” induces a voltage drop across the inductor: as electrons want to flow from left to right, we say the left side of the inductor is more negative than the right side. The voltage drop has therefore reversed, but it did not occur immediately, nor will it last forever, because the system will oscillate: as the electrons on the left move to the right, they cause a magnetic field to build up in the inductor, and the process repeats ad infinitum.
Adding to the explanation, we can recognise a build-up of charge as a capacitor. There is always parasitic capacitance because charge can always accumulate in a section of wire. Therefore, there is no such thing as a perfect inductor (for if there were, we could not disconnect it!). Rather, an actual inductor can be modelled by an ideal inductor in parallel with an ideal capacitor. (Technically, there should also be a resistor in series to model the inevitable loss in ordinary inductors.) An inductor and capacitor in parallel form what is known as a resonant “LC” circuit, which, as the name suggests, resonates!
Intuition behind Caratheodory’s Criterion: Think “Sharp Knife” and “Shrink Wrap”!
Despite many online attempts at providing intuition behind Caratheodory’s criterion, I have yet to find an answer to why testing all sets should work.
- https://www.thestudentroom.co.uk/showthread.php?t=4284694
- https://mathoverflow.net/questions/34007/demystifying-the-caratheodory-approach-to-measurability
Therefore, I have taken the liberty of proffering my own intuitive explanation. For the impatient, here is the gist. Justification and background material are given later.
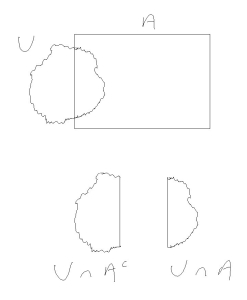
The set U is non-measurable. The set A is measurable.
We will think of our sets as rocks. As explained later, a rock is not “measurable” if its boundary is too jagged. In the above image, the rock is not measurable because it has a very jagged boundary. On the other hand, the rock
has a very nice boundary and hence we would like to consider
to be “measurable”.
For to be measurable according to Caratheodory’s criterion, the requirement is for
to hold for all sets
. While other references generally make it clear that this is a sensible requirement if
is measurable (and we will go over this below), what makes Caratheodory’s criterion unintuitive is the requirement that
must hold for all sets
, including non-measurable sets. However, we argue that a simple change in perspective makes it intuitively clear why we can demand
holds for all
.
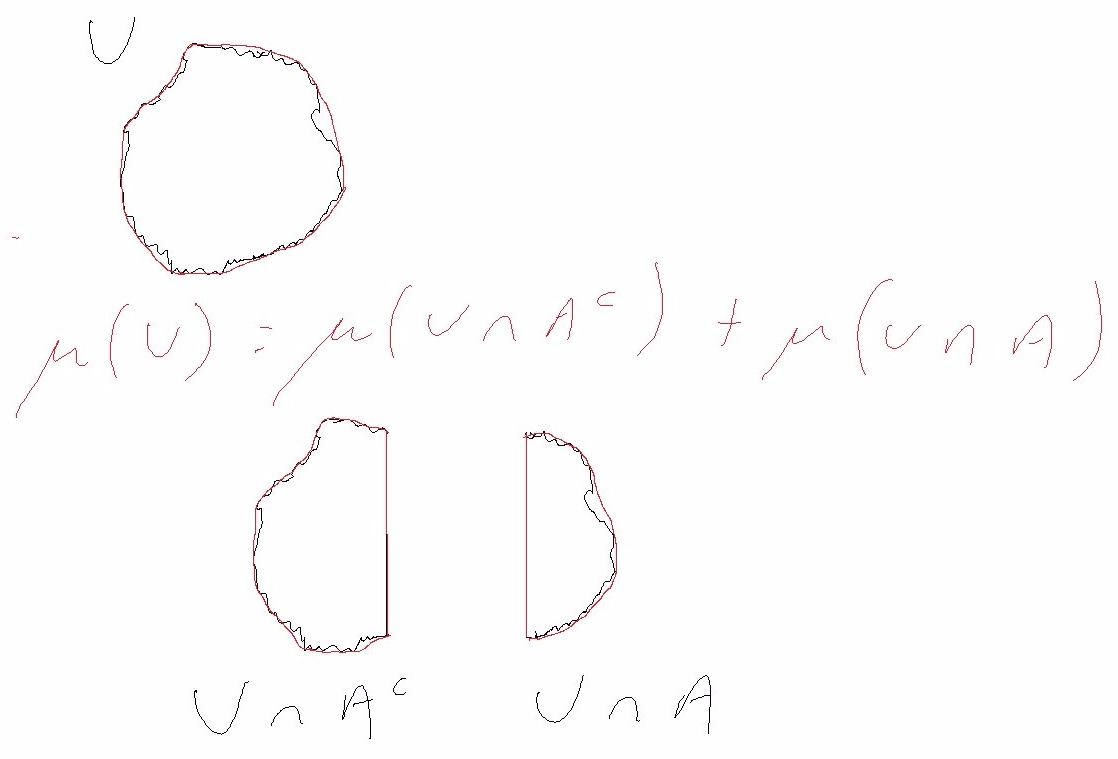
An outer measure uses shrink wrap to approximate the boundary. If A cuts the rock U cleanly then the same “errors” are made when approximating the boundaries of the three objects in the picture, hence Caratheodory’s criterion holds.
The two ingredients of our explanation are that the boundary of serves as a knife, and that an outer measure calculates volume by using shrink wrap. (For example, Lebesgue outer measure approximates a set by a finite union of cubes that fully cover the set, and uses the volume of the cubes as an estimate of the volume of the set; precisely, the infimum over all such approximations is used.)
In the above image, the red curve represents the shrink wrap. The outer measure is given by the area enclosed by the red curve. (For rocks, which are three dimensional, we would use the volume encased by the shrink wrap.)
When we take and
, we think of using part of the boundary of
(the part that intersects
) to cut
. If
is a rectangle (or cube) then we produce a very clean straight cut of the set (or rock)
.
Consider shrink wrapping and
individually, as shown by the red curves in the above image. Two observations are critical.
- If the cut made by
is clean then the shrink wrap fits the cut perfectly; no error is made for this part of the boundaries of
and
.
- For all other parts of the boundaries of
and
(i.e., the jagged parts), the errors made by the shrink wrap for
and
precisely equal the errors made by the shrink wrap for
(because it is the same jagged boundary being fitted).
It follows that holds whenever
has a nice boundary.
Regardless of whether is measurable or not, Caratheodory’s criterion is blind to the boundary of
and instead is only testing how “smooth” the boundary of
is. (Different sets
will test different parts of the boundary of
.)
From the Beginning
First, it should be appreciated that Caratheodory’s criterion is not magical: it cannot always produce the exact sigma-algebra that you are thinking of, so it suffices to understand why, in certain situations, it is sensible. In particular, this means we can assume that the outer measure we are given, works by considering approximations of a given set by larger but nicer sets, such as finite collections of open cubes, whose measure we know how to compute. Taking the infimum of the measures of these approximating sets gives the outer measure of
.
In physical terms, think of measuring the volume of rocks. An outer measure works by wrapping shrink wrap as tightly as possible around the rock, then asking for the volume encased by the shrink wrap. The key point is that if the boundary of the rock is piecewise smooth then the shrink wrap computes its exact volume, whereas if the boundary is sufficiently jagged then the shrink wrap cannot follow the contours perfectly and the shrink wrap (i.e., the outer measure) will exaggerate the true volume of the rock.
It is easy to spot rocks with bad boundaries if the volume of the whole space is finite: look at both the rock and its complement. Place shrink wrap over both of them. If the shrink wrap can follow the contours then it will measure the volume of the two interlocking parts perfectly and the sum of the volumes will equal the volume of the whole space. If not, we know the rock is too ill-shaped to be considered measurable.
If the total volume is infinite then we must zoom in on smaller portions of the boundary. For example, we might take an open ball and look at the boundary of
using our shrink wrap trick: shrink wrap both
and its complement in
, namely,
, and see if the volumes of
and
add up to the volume of
. If not, we know
is too ill-shaped to be considered measurable. This seemingly relies on our choice of
being a sufficiently nice/benign shape that it does not interfere with our observation of the boundary of
. For Lebesgue outer measure, the choice of an open ball for
seems entirely appropriate, but perhaps the right choice will depend on the particular outer measure under consideration. Caratheodory’s criterion removes the need for such a choice by requiring
to hold for all
and not just nice
. The images and explanation given at the start of this note explain why this works: the jaggedness of
appears on both sides of the equation and cancels out, therefore Caratheodory’s criterion is really only testing the boundary of
.
Remarks
- Of course, intuition must be backed up by rigorous mathematics, and it turns out that Caratheodory’s criterion is useful because it is easy to work with and produces the desired sigma-algebra in many situations of interest.
- Our intuitive argument has focused on the boundary of sets. If we consider a Borel measure (one generated by the open sets of a topological space) then we know that open sets are measurable and hence it is indeed the behaviour at the boundary that matters. That said, intuition need not be perfect to be useful.
An Alternative (and Very Simple) Derivation of the Boltzmann Distribution
This note gives a very simple derivation of the Boltzmann distribution that avoids any mention of temperature or entropy. Indeed, the Boltzmann distribution can be understood as the unique distribution with the property that when a large (or even a small!) number of Boltzmann distributions are added together, all the different ways of achieving the same “energy” have the same probability of occurrence, as now explained.
For the sake of a mental image, consider a small volume of gas. This small volume can take on three distinct energy levels, say, 0, 1 and 2. Assume the choice of energy level is random, with corresponding probabilities and
. A large volume of the gas can be partitioned into many such small volumes, and the total energy is simply the sum of the energies of each of the small volumes.
Mathematically, let denote the number of small volumes and let
denote the energy of the
th small volume, where
ranges from 1 to
. The total energy of the system is
.
For a fixed and a fixed total energy
, there may be many outcomes
with the prescribed energy
. For example, with
and
, the possibilities are
. The probabilities of these possibilities are
respectively. Here, we assume the small volumes are independent of each other (non-interacting particle model). Can we choose
so that all the above probabilities are the same?
Since the ordering does not change the probabilities, the problem reduces to the following. Let and
denote the number of small volumes which are in energy levels 0, 1 or 2 respectively. Then
and
. For fixed
and
, we want
to be constant for all valid
.
A brute-force computation is informative: write and
. Then
. This will be independent of
if and only if
is constant, or in other words,
. Remarkably, this is valid in general, even for small
.
Up to a normalising constant, the solutions to are parametrised by
and
. Varying
varies the average energy of the system. Letting
, we can reparametrise the solutions by
. (Check:
;
; and
.) This is indeed the Boltzmann distribution when the energy levels are 0, 1 or 2.
More generally, we can show that the Boltzmann distribution is the unique distribution with the property that different configurations (or “microstates”) having the same and
have the same probability of occurrence. In one direction, consider the (unnormalised) probabilities
that define the Boltzmann distribution. Then
where
is the total energy of the system. (Here, the
th region has energy
, and there are precisely
regions with this energy in the configuration under consideration.) Therefore, the probability of any particular configuration depends only on the total energy and is thus uniformly distributed conditioned on the total energy being known. In the other direction, although we omit the proof, we can derive the Boltzmann distribution in generality along the same lines as was done earlier for three specific energy levels: regardless of the total number of energy levels, it suffices to consider in turn the energy levels
and
with probabilities
and
. Assuming the
are zero except for
then leads to a constraint on
as a function of
.
Some Comments on the Situation of a Random Variable being Measurable with respect to the Sigma-Algebra Generated by Another Random Variable
If is a
-measurable random variable then there exists a Borel-measurable function
such that
. The standard proof of this fact leaves several questions unanswered. This note explains what goes wrong when attempting a “direct” proof. It also explains how the standard proof overcomes this difficulty.
First some background. It is a standard result that where
is the set of all Borel subsets of the real line
. Thus, if
then there exists an
such that
. Indeed, this follows from the fact that since
is
-measurable, the inverse image
of any Borel set
must lie in
.
A “direct” proof would endeavour to construct pointwise. The basic intuition (and not difficult to prove) is that
must be constant on sets of the form
for
. This suggests defining
by
. Here, the supremum is used to go from the set
to what we believe to be its only element, or to
if
is empty. Unfortunately, this intuitive approach fails because the range of
need not be Borel. This causes problems because
is the range of
and must be Borel if
is to be Borel-measurable.
Technically, we need a way of extending the definition of from the range of
to a Borel set containing the range of
, and moreover, the extension must result in a measurable function.
Constructing an appropriate extension requires knowing more about than simply
for each individual
. That is, we need a canonical representation of
. Before we get to this though, let us look at two special cases.
Consider first the case when for some measurable set
, where
is the indicator function. If
is
-measurable then
must lie in
and hence there exists a Borel
such that
. Let
. (It is Borel-measurable because
is Borel.) To show
, let
be arbitrary. (Recall, random variables are actually functions, conventionally indexed by
.) If
then
and
, while
because
. Otherwise, if
then analogous reasoning shows both
and
equal zero.
How did the above construction avoid the problem of the range of not necessarily being Borel? The subtlety is that the choice of
need not be unique, and in particular,
may contain values which lie outside the range of
. Whereas a choice such as
assigns a single value (in this case,
) to values of
not lying in the range of
, the choice
can assign either
or
to values of
not in the range of
, and by doing so, it can make
Borel-measurable.
Consider next the case when . As above, we can find Borel sets
such that
for
, and moreover,
gives a suitable
. Here, it can be readily shown that if
is in the range of
then
can lie in at most one
. Thus, regardless of how the
are chosen,
will take on the correct value whenever
lies in the range of
. Different choices of the
can result in different extensions of
, but each such choice is Borel-measurable, as required.
The above depends crucially on having only finitely many indicator functions. A frequently used principle is that an arbitrary measurable function can be approximated by a sequence of bounded functions with each function being a sum of a finite number of indicator functions (i.e., a simple function). Therefore, the general case can be handled by using a sequence of random variables converging pointwise to
. Each
results in an
obtained by replacing the
by
, as was done in the paragraph above. For
in the range of
, it turns out as one would expect: the
converge, and
gives the correct value for
at
. For
not in the range of
, there is no reason to expect the
to converge: the choice of the
at the
th and
th steps are not coordinated in any way when it comes to which values to include from the complement of the image of
. Intuitively though, we could hope that each
includes a “minimal” extension that is required to make
measurable and that convergence takes place on this “minimal” extension. Thus, by choosing
to be zero whenever
does not converge, and choosing
to be the limit of
otherwise, we may hope that we have constructed a suitable
despite how the
at each step were chosen. Whether or not this intuition is correct, it can be shown mathematically that
so defined is indeed the desired function. (See for example the short proof of Theorem 20.1 in the second edition of Billingsley’s book Probability and Measure.)
Finally, it is remarked that sometimes the monotone class theorem is used in the proof. Essentially, the idea is exactly the same: approximate by a suitable sequence
. The subtlety is that the monotone class theorem only requires us to work with indicator functions
where
is particularly nice (i.e.,
lies in a
-system generating the
-algebra of interest). The price of this nicety is that
must be bounded. For the above problem, as Williams points out in his book Probability with Martingales, we can simply replace
by
to obtain a bounded random variable. On the other hand, there is nothing to be gained by working with particularly nice
, hence Williams’ admission that there is no real need to use the monotone class theorem (see A3.2 of his book).
Poles, ROCs and Z-Transforms
Why should all the poles be inside the unit circle for a discrete-time digital system to be stable? And why must we care about regions of convergence (ROC)? With only a small investment in time, it is possible to gain a very clear understanding of exactly what is going on — it is not complicated if learnt step at a time, and there are not many steps.
Step 1: Formal Laurent Series
Despite the fancy name, Step 1 is straightforward. Digital systems operate on sequences of numbers: a sequence of numbers goes into a system and a sequence of numbers comes out. For example, if denotes an input sequence then an example of a discrete-time system is
.
How can a specific input sequence be written down, and how can the output sequence be computed?
The direct approach is to specify each individual , for example,
for
,
,
,
and
for
. Direct substitution then determines the output:
,
and so forth.
The system has a number of nice properties, two of which are linearity and time invariance. This is often expressed in textbooks by saying the system is LTI, where the L in LTI stands for Linear and the TI stands for Time Invariant. When first learning about discrete-time digital systems, usually attention is restricted to linear time-invariant systems, and indeed, it is for such systems that the Z-transform proves most useful.
Any LTI system has the property that the output is the convolution of the input with the impulse response. For example, the impulse response of is found by injecting the input
and
for
. This impulse as input produces the output
,
and
for
. It is common to denote the impulse response using the letter
, that is,
,
and
for
.
By the definition of convolution, the convolution of a sequence with a sequence
is
. If
,
and
for
then
and this is equal to
; we have verified in this particular case that the output of the original system is indeed given by convolving the input with the impulse response.
Let’s be honest: writing ,
and
for
is tedious! An alternative is to use a formal Laurent series to represent a sequence. Here, “formal” means that we do not try to evaluate this series! A Laurent series just means instead of limiting ourselves to polynomials in a dummy variable
, we allow negative powers of
, and we allow an infinite number of non-zero terms. (The variable
has nothing to do with time; it will be replaced in Step 3 by
where it will be referred to as the Z-transform. To emphasise,
is just a dummy variable, a placeholder.)
Precisely, the sequence ,
and
for
can be encoded as
; isn’t that much more convenient to write? In general, an arbitrary sequence
can be encoded as the formal series
. The sole purpose of the
term is as a placeholder for placing the coefficient
. In other words, if we are given the formal series
then we immediately know that that is our secret code for the sequence that consists of all zeros except for the -5th term which is 2, the 0th term which is 3 and the 7th term which is 1.
Being able to associate letters with encoded sequences is convenient, hence people will write to mean
,
,
and
for
. Do not try to evaluate
for some value of
though – that would make no sense at this stage. (Mathematically, we are dealing with a commutative ring that involves an indeterminant
. If you are super-curious, see Formal Laurent series.)
Now, there is an added benefit! If the input to our system is and the impulse response is
then there is a “simple” way to determine the output: just multiply these two series together! The multiplication rule for formal Laurent series is equivalent to the convolution rule for two sequences. You can check that
(corresponding to
etc) really is the output of our system if the input were
for
,
,
,
and
for
.
- A formal Laurent series provides a convenient encoding of a discrete-time sequence.
- Convolution of sequences corresponds to multiplication of formal Laurent series.
- Do not think of formal Laurent series as functions of a variable. (They are elements of a commutative ring.) Just treat the variable as a placeholder.
- In particular, there is no need (and it makes no sense) to talk about ROC (regions of convergence) if we restrict ourselves to formal Laurent series.
Step 2: Analytic Functions
This is where the fun begins. We were told not to treat a formal Laurent series as a function, but it is very tempting to do so… so let’s do just that! 🙂 The price we pay though is that we do need to start worrying about ROC (regions of convergence) for otherwise we could end up with incorrect answers.
To motivate further our desire to break the rules, consider the LTI system . Such a system has “memory” or an “internal state” because the current output
depends on a previous output
and hence the system must somehow remember previous values of the output. We can assume that in the distant past the system has been “reset to zero” and hence the output will be zero up until the first time the input is non-zero. The impulse response is determined by setting
to 1 and observing the output:
,
,
and in general
for
. Encoding this using a formal Laurent series gives the alternative representation
.
There is a more “efficient” representation of based on the Taylor series expansion
. Indeed, if we were to break the rules and treat
as a function, we might be tempted to write
instead of
. It turns out that, with some care, it is mathematically legitimate to do this. (Furthermore, Step 3 will explain why it is beneficial to go to this extra trouble.)
We know we can encode a sequence using a formal Laurent series, and we can reverse this operation to recover the sequence from the formal Laurent series. In Step 2 then, we just have to consider when we can encode a formal Laurent series as some type (what type?) of function, meaning in particular that it is possible to determine uniquely the formal Laurent series given the function.
Power series (and Laurent series) are studied in complex analysis: recall that every power series has a (possibly zero) radius of convergence, and within that radius of convergence, a power series can be evaluated. Furthermore, within the radius of convergence, a power series (with real or complex coefficients) defines a complex analytic function. The basic idea is that a formal Laurent series might (depending on how quickly the coefficients die out to zero) represent an analytic function on a part of the complex plane.
If the formal Laurent series only contains non-negative powers of then it is a power series
and from complex analysis we know that there exists an
, the radius of convergence (which is possibly zero or possibly infinite), such that the sum converges if
and the sum diverges if
. In particular,
is an analytic function on the open disk
.
If the formal Laurent series only contains non-positive powers, that is, , then we can consider it to be a power series in
and apply the above result. Since
, there exists a
(possibly zero or possibly infinite) such that
is an analytic function on
. [From above, the condition would be
which is equivalent to
hence defining
verifies the claim.]
In the general case, a formal Laurent series decomposes as . Both sums must converge if it is to define an analytic function, hence in the general case, a formal Laurent series defines an analytic function on a domain of the form
.
The encoding of a sequence as an analytic function is therefore straightforward in principle: given a formal Laurent series , determine the constants
and
, and provided the region
is non-empty, we can use the analytic function
to encode the sequence
. We must specify the ROC
together with
whenever we wish to define a sequence in this way; without knowing the ROC, we do not know the domain of definition of
, that is, we would not know for what values of
does
describe the sequence we want. It is possible for a function
to describe different sequences depending on the ROC! An example of this is now given.
If then we have seen that
. But wait! This is not entirely true. If
then certainly
.Yet if
then
. The function
for
does not describe the series
. It looks like a perfectly good function though, so what series does it describe?
The region is unbounded. (In fact, it is an open disc centred at the point at infinity.) This motivates us to replace
by
so that the domain becomes
and we can attempt looking for a power series in
. Precisely,
. Therefore, the single function
actually encodes two different series depending on whether we treat it as a function on
or a function on
.
Readers remembering their complex analysis will not find this bizarre because a holomorphic (i.e., complex differentiable) function generally requires more than one power series to represent it. A power series about a point is only valid up until a pole is encountered, after which another point must be chosen and a power series around that point used to continue the description of the function. When we change points, the coefficients of the power series will generally change. In the above example, the first series is a power series around the origin while the second series
is a power series around the point at infinity and therefore naturally has different coefficients. (Thankfully there are only these two possibilities to worry about: a power series about a different point
would look like
and is not of the form we described in Step 1. Only when
or
does the power series match up with the formal Laurent series in Step 1.)
While it might seem that introducing analytic functions is an unnecessary complication, it actually makes certain calculations simpler! Such a phenomenon happened in Step 1: we discovered convolution of sequences became multiplication of Laurent series (and usually multiplication is more convenient than convolution). In Step 3 we will see how the impulse response of can be written down immediately.
Step 3: The Z-transform
Define and
. Clearly, the constraint
implies a relationship between
and
, but how can we determine this relationship?
Note that is actually an infinite number of constraints, one for each
. The first step is to think of these as a single constraint on the whole sequences
and
. We can do this either intuitively or rigorously, arriving at the same answer either way.
Intuitively, think of a table (my lack of WordPress skills prevents me from illustrating this nicely). The top row looks like . The next row looks like
. The last row looks like
. Stack these three rows on top of each other so they line up properly: the purpose of the table is to line everything up correctly! Then another way of expressing
is by saying that the first row of the table is equal to the second row of the table plus the third row of the table, where rows are to be added elementwise.
Rigorously, what has just happened is that we are treating a sequence as a vector in an infinite-dimensional vector space: just like is a vector in
, we can think of
as a vector in
. Each of the three rows of the table described above is simply a vector.
To be able to write the table compactly in vector form, we need some way of going from the vector to the shifted-one-place-to-the-right version of it, namely
. In linear algebra, we know that a matrix can be used to map one vector to another vector provided the operation is linear, and in fact, shifting a vector is indeed a linear operation. In abstract terms, there exists a linear operator
that shifts a sequence one place to the right:
.
Letting and
denote the vectors
and
respectively, we can rigorously write our system as
. This is precisely the same as what we did when we said the first row of the table is equal to the second row of the table plus the third row of the table.
Our natural instinct is to collect like terms: if denotes the identity operator (think of a matrix with ones on the diagonal), so that
, then
is equivalent to
, that is,
. This equation tells us the output
as a function of the input
— but how useful is it? (Does the inverse
exist, and even if it does, how can we evaluate it?)
While in some cases the expression might actually be useful, often it is easier to use series rather than vectors to represent sequences: we will see that the linear operator
is equivalent to multiplication by
, which is very convenient to work with!
Precisely, since and
represent exactly the same sequence, it should be clear that the equation
is equivalent to the equation
. Indeed, returning to the table,
corresponds to the first row,
corresponds to the last row, and
corresponds to the second row.
Now, from Step 2, we know that we can think of and
as analytic functions (provided we are careful about the ROC). Therefore, we feel entitled to continue manipulating
to obtain
. Since by definition the impulse response
satisfies
, we seem to have immediately found the impulse response
of the original system; at the very least, it agrees with the longer calculation performed at the start of Step 2.
Remark: Actually, the only way to justify rigorously that the above manipulation is valid is to check the answer we have found really is the correct answer. Indeed, to be allowed to perform the manipulations we must assume the existence of a domain on which both and
are analytic. If we assume
is “nice” then, under that assumption, prove that
is “nice”, that does not mean
is nice. It is like saying “if it is raining then we can show it really is raining, therefore it must be raining right now!”. A rigorous justification would look something like the following. First we must make some assumption about the input sequence for otherwise we have no idea what ROC to use. If we are interested in inputs that are uniformly bounded and which are zero up until time 0 then we can safely assume that
is analytic on
. Since
is non-zero whenever
, we know
is analytic on
. Therefore
will be analytic on
. This means that
can be expanded as a power series in a neighbourhood of the origin, and the coefficients of that power series are what we believe the output of the system will be. To check this really is the output of the system, it suffices to show
for
. This is straightforward:
as required, where every manipulation can be seen to be valid for
(there are no divisions by zero or other bad things occurring).
The remark above shows it is (straightforward but) tedious to verify rigorously that we are allowed to perform the manipulations we want. It is much simpler to go the other way and define a system directly in terms of and its ROC. Then, provided the ROC of
overlaps with the ROC of
, the output
is given by
on the overlap, which can be correctly expanded as a Laurent series with regard to the ROC, and the output sequence read off.
All that remains is to introduce the Z-transform and explain why engineers treat as a “time shift operator”.
The Z-transform is simply doing the same as what we have been doing, but using instead of
. Why
rather than
? Just convention (and perhaps a bit of convenience too, e.g., it leads to stable systems being those with all poles inside the unit circle, rather than outside). In fact, sometimes
is used instead of
, hence you should always check what conventions an author or lecturer has decided to adopt.
The rule that engineers are taught is that when you “take the Z-transform” of then you replace
by
,
by
and
by
. The reason this rule works was justified at great length above: recall that as an intermediate mental step we can think of the input and output as vectors, and this led to thinking of them instead as series, because multiplication by
will then shift the sequence one place to the right. Thus,
is asserting that the sequence
is equal to the sequence
plus a half times the sequence
shifted to the right by one place, which is equivalent to the original description
.
Step 4: Poles and Zeros
A straightforward but nonetheless rich class of LTI systems can be written in the form . Importantly, this class is “closed” in that if you connect two such systems together (the output of one connects to the input of the other) then the resulting system can again be written in the same way (but generally with larger values of
). Another important feature of this class of systems is that they can be readily implemented in hardware.
Applying the Z-transform to such a system shows that the impulse response in the Z-domain is a rational function. Note that the product of two rational functions is again a rational function, demonstrating that this class of systems is closed under composition, as stated above. Most of the time, it suffices to work with rational impulse responses.
If is rational (and in reduced form — no common factors) then the zeros of
are the solutions of the polynomial equation
while the poles are the solutions of the polynomial equation
. [More generally, if
is analytic, then the zeros are the solutions of
and the poles are the solutions of
.] Note that a pole of
is a zero of its inverse: if we invert a system, poles become zeros and zeros become poles.
Poles are important because poles are what determine the regions of convergence and hence they determine when our manipulations in Step 3 are valid. This manifests itself in poles having a physical meaning: as we will see, the closer a pole gets to the unit circle, the less stable a system becomes.
Real-world systems are causal: the output cannot depend on future input. The impulse response of a causal system is zero for
. Therefore, the formal Laurent series (Step 1) representation of
has no negative powers of
. Its region of convergence will therefore be of the form
for some
. (If
then the system would blow up!) Since
, the ROC of a causal transfer function
will therefore be of the form
for some
. If
is rational then it has only a finite number of poles, and it suffices to choose
to be the largest of the magnitudes of the poles.
Let’s look at an unstable system: . This system is clearly unstable because its impulse response is readily seen to be
. We put in a bounded signal (
and
for
) yet obtain an unbounded output (
for
). Taking the Z-transform gives
, so that
. For
, this gives us the correct series representation
.
If we put a signal that starts at time zero (i.e., for
) into a causal system we will get an output even if the system is unstable. This is because the input
will have a ROC of the form
and
has a ROC of the form
, so
will have a ROC
.
If we put a signal that started at time into our system, then there might be no solution! (Intuitively, it means the system will have to have blown up before reaching time 0.) For example,
with ROC
represents the signal
for
and
for
. We cannot form the product
because there is no value of
for which both
and
are valid: one’s ROC is
while the other’s is
.
There are many different definitions of a sequence being bounded. Three examples are: 1) there exists an such that, for all
,
; 2)
; and 3)
. Out of these three, the easiest to detect whether
is bounded given only
is the second one: if the ROC of
includes
then, by definition (see a complex analysis textbook),
is absolutely convergent for
, meaning
, hence
because
implies
for all
. This type of boundedness is called “bounded in
“. For the reverse direction, recall that the radius of convergence
is such that a power series in
will converge for all
and diverge for all
. Therefore, if the boundary of the largest possible ROC of
does not contain the unit circle then
must be unbounded in
. (The boundary case is inconclusive: the power series
has a ROC
yet
is bounded. On the other hand,
has a ROC
and
is unbounded.)
A sequence is bounded in
if the largest possible ROC of
includes the unit circle
. A sequence
is unbounded in
if the closure of the largest possible ROC does not include the unit circle.
If the ROC of the transfer function includes the unit circle, then an
-bounded input will produce an
-bounded output. Indeed, the ROC of both
and
will include the unit circle, therefore, the ROC of
will include the unit circle and
will be
-bounded.
If all the poles of a causal are within the unit circle then the ROC will include the unit circle, hence a bounded input will produce a bounded output. Engineers therefore call a system stable if all the poles of
are inside the unit circle.
Note that it follows from earlier remarks that if has a pole outside the unit circle then the impulse response will be unbounded. If
has a pole on the unit circle then the impulse response will resonant at the corresponding frequency indefinitely. For example, if
where
then
for
. This does not die away because
for all
. By writing
we get
and therefore we think of this as a resonance at frequency
. Furthermore, if
where
, then
and we see that there is a damped resonance at frequency
. As the pole gets closer to the unit circle (that is,
) the impulse response takes longer to die out. Engineers care about pole placement!
Epilogue
- Although often engineers can get away with just following recipes, it is safer in the long run and easier to remember the recipes if you have spent a bit more time to learn the underlying rationale for when and why the rules work.
- Linear algebra and complex analysis are considered core subjects of an undergraduate mathematics degree because they have such broad applicability: here we saw them play integral roles in discrete-time signal processing.
- This is because the “mathematical behaviour” of Laurent series matches the “physical behaviour” of discrete-time linear time-invariant systems.
- There is a close relationship between the Z-transform and the Fourier transform: just make the substitution
. This is only allowed if the ROC contains the unit circle. The concept of a pole does not explicitly appear in the Fourier domain because, rather than permit
to be anywhere in the complex plane, the substitution
means we are only looking at the behaviour of
on the unit circle.
- When it comes to system design, understanding where the poles and zeros are can be more productive than trying to understand the whole frequency spectrum.